一、模型的选取
房地产市场的运行过程非常错综复杂,它既受到市场供求关系的影响,又受外界宏观政策的调控。因此在研究房地产市场时,研究的多是房地产价格指数,其变化能直接反映房地产市场变化发展趋势,对此类数据建立相应的数学模型来研究是合适的。
在价格预测方面,常常是对房价数据建立一般线性时间模型,再进行短期预测。时间序列是将符合某一指标的数据按时间发生的先后顺序排列,排列可以按年度、季度、月度或其他时间形式,这些数列由于随机因素的影响,自身表现出随机偶然性,数列成员之间存在依存关系。序列整体呈现出序列之间的动态性特征,我们称其为时间序列的记忆性,具体表现为:即使数据的时间间隔很大,也能呈现出某种相关性。一般的线性时间序列模型是由自回归滑动平均模型,即ARMA(p,q)构成。
自回归模型(简称AR模型),是统计上一种处理时间序列的方法,用同一变数例如x的之前各期,亦即x1至xt-1来预测本期xt的表现,并假设它们为一线性关系。因为这是从回归分析中的线性回归发展而来,只是不用x预测y,而是用x预测 x(自己);所以叫做自回归。
![]()
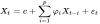
在进行时间序列分析时,我们只考虑变量之间自身发展的影响性,在建立时间序列模型来预测未来时,并不考虑影响变量的外部相关因数,要建立ARMA模型,样本数据必须是平稳序列。因而第一步就需要对序列进行相关性检验,若序列平稳,则可以直接建立ARMA模型,若数据不平稳,需要对其进行一阶差分或者取对数再一阶差分,将不平稳序列转化为平稳序列。在第一步得到平稳之后需要对其进行相关性检验,因为不是所有的平稳性序列都可以建立ARMA模型,若序列的成员之间没有相关性,即过去的信息不会对未来变化产生影响,说明此序列是纯随机序列,在统计意义上,没有什么研究价值。若序列成员之间存在相关性,过去的表现对未来变化有一定影响时,我们才能根据过去的信息预测未来。在建立ARMA模型之后,需要对模型残差进行相关性检验,检验残差序列是否是白噪音。
二、模型的建立
房地产价格受多种因素的影响,但是很多因素难以量化,比如房地产的周边环境、国家的制度政策、购买者的心理偏好等等,因此本文舍弃这些难以量化的因素,选取10个影响房价的可度量的主要影响因素,见表1。
表1 指标选取
指标名称 | 指标参数 | |
主要影响因数 | 国内生产总值(亿元) | X1 |
居民消费水平(元) | X2 | |
城镇人口数(万人) | X3 | |
房地产住宅投资(亿元) | X4 | |
房地产开发企业土地成交价款(亿元) | X5 | |
房地产开发投资额(亿元) | X6 | |
居民销售价格指数(上年=100) | X7 | |
居民人均居住消费支出(元) | X8 | |
房地产开发企业国内贷款(亿元) | X9 | |
一年贷款利率(%) | X10 | |
选取 2010年-2019年的全国商品房平均销售价格作为被解释变量, 记为Y。10个变量的数据均由国家统计局官网查询得到。详细数据见表2。
表22000年-2019年全国新房平均销售价格及影响因素数据(1)
年份 | 在售新房样本均价(元/平方米) | 国内生产总值(亿元) | 居民消费水平(元) | 城镇人口数(万人) | 房地产住宅投资 (亿元) |
2010 | 9094 | 412119.3 | 10550 | 66978 | 34026.23 |
2011 | 9709 | 487940.2 | 12646 | 69079 | 44319.51 |
2012 | 9628 | 538580 | 14075 | 71182 | 49374.21 |
2013 | 10321 | 592963.2 | 15615 | 73111 | 58950.76 |
2014 | 10817 | 643563.1 | 17271 | 74916 | 64352.15 |
2015 | 10697 | 688858.2 | 18929 | 77116 | 64595.24 |
2016 | 12005 | 746395.1 | 20877 | 79298 | 68703.87 |
2017 | 13584 | 832035.9 | 23070 | 81347 | 75147.88 |
2018 | 14362 | 919281.1 | 25378 | 83137 | 85124.02 |
2019 | 14922 | 990865.1 | 27563 | 84843 | 97070.74 |
表22000年-2019年全国新房平均销售价格及影响因素数据(2)
年份 | 房地产开发企业土地成交价款 (亿元) | 房地产开发投资额 (亿元) | 居民销售价格指数 (上年=100) | 居民人均居住消费支出 (元) | 房地产开发企业国内贷款 (亿元) | 一年贷款利率(%) |
2010 | 8206.71 | 48259.4 | 103.3 | 12563.7 | 5.35 | |
2011 | 8894.03 | 61796.89 | 105.4 | 13056.8 | 6.35 | |
2012 | 7409.64 | 71803.79 | 102.6 | 14778.39 | 6.26 | |
2013 | 9918.29 | 86013.38 | 102.6 | 2999 | 19672.66 | 5.6 |
2014 | 10019.88 | 95035.61 | 102 | 3201 | 21242.61 | 5.97 |
2015 | 7621.61 | 95978.85 | 101.4 | 3419 | 20214.38 | 4.98 |
2016 | 9129.31 | 102580.61 | 102 | 3746 | 21512.4 | 4.9 |
2017 | 13643.39 | 109798.53 | 101.6 | 4107 | 25241.76 | 4.9 |
2018 | 16102.16 | 120164.75 | 102.1 | 4647 | 24132.14 | 5.43 |
2019 | 14709.28 | 132194.26 | 102.9 | 5055 | 25228.77 | 4.85 |
三、因子分析
(一)适应性检验
数据量小于变量数,不可进行适应性检验分析。
(二)提取因子变量
在上述分析的基础上,利用 SPSS22.0软件进行主成分因子提取,得到各因子的特征值和贡献率,根据因子提取原则,本文提取前2个因子,其对总方差的贡献率达到91.141,能够较好地作为公因子代表所选取的10个指标,以达到因子分析降维的目的。同时从因子分析的碎石图中也可以看出,在第2个因子处的拐点最为明显,因此本文提取前2个因子进行下一步的研究与探讨。
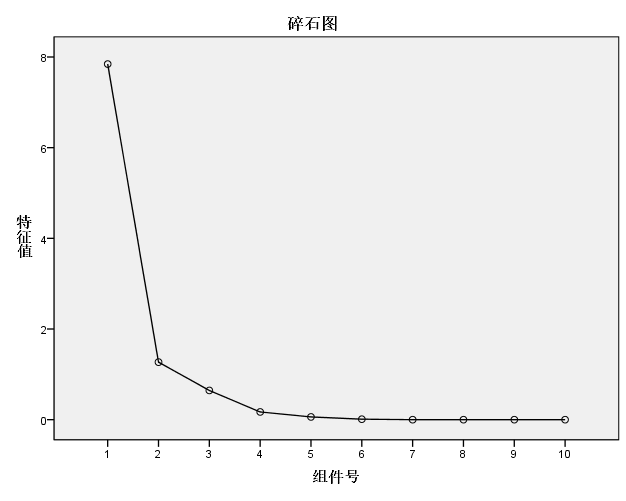
图1 碎石图
表3解释的总方差
成份 | 初始特征值 | 提取平方和载入 | 旋转平方和载入 | ||||||
合计 | 方差的% | 累计% | 合计 | 方差的% | 累计% | 合计 | 方差的% | 累计% | |
1 | 7.845 | 78.445 | 78.445 | 7.845 | 78.445 | 78.445 | 7.836 | 78.364 | 78.364 |
2 | 1.270 | 12.696 | 91.141 | 1.270 | 12.696 | 91.141 | 1.278 | 12.776 | 91.141 |
3 | .644 | 6.444 | 97.585 | ||||||
4 | .170 | 1.703 | 99.288 | ||||||
5 | .061 | .608 | 99.896 | ||||||
6 | .010 | .104 | 100.000 | ||||||
7 | 100.000 | ||||||||
8 | 100.000 | ||||||||
9 | 100.000 | ||||||||
10 | 100.000 | ||||||||
(三)建立因子载荷矩阵
提取主因子后建立载荷矩阵,由于初始矩阵的公共因子在各数据指标上的载荷较为接近,对公共因子分类的分析造成困难,故采用运用方差最大法对因子进行正交旋转处理,并以此创建因子载荷矩阵,以达到公共因子能更好地反映其各自经济含义的目的,旋转后的因子载荷矩阵见表4.
表4 因子载荷矩阵表
成分 | ||
1 | 2 | |
国内生产总值(亿元) | .998 | -.001 |
居民消费水平(元) | .996 | -.050 |
居民人均居住消费支出(元) | .995 | .040 |
房地产开发投资额(亿元) | .988 | .070 |
城镇人口数(万人) | .986 | -.138 |
房地产住宅投资(亿元) | .975 | .156 |
房地产开发企业国内贷款(亿元) | .927 | -.009 |
房地产开发企业土地成交价款(亿元) | .846 | .353 |
居民销售价格指数(上年=100) | .293 | .803 |
一年贷款利率(%) | -.547 | .675 |
提取方法:主成份分析。 | ||
a. 旋转在 3次迭代后已收敛。 | ||
(四)计算各因子得分
由SPSS软件计算得到各因子得分系数矩阵如表5所示,由此可以得到四个因子的数学表达式为:
表5 成份得分系数矩阵
成分 | ||
1 | 2 | |
国内生产总值(亿元) | .128 | -.024 |
居民消费水平(元) | .129 | -.062 |
城镇人口数(万人) | .130 | -.132 |
房地产住宅投资(亿元) | .121 | .100 |
房地产开发企业土地成交价款(亿元) | .100 | .258 |
房地产开发投资额(亿元) | .125 | .032 |
居民销售价格指数(上年=100) | .019 | .625 |
居民人均居住消费支出(元) | .127 | .009 |
房地产开发企业国内贷款(亿元) | .119 | -.028 |
一年贷款利率(%) | -.086 | .544 |
提取方法:主成份分析。 | ||
F1=0.128x1+0.129x2+0.13x3+0.121x4+0.1x5+0.125x6+0.019x7+0.127x8+0.119x9-0.086x10
F2=-0.024x1-0.062x2-0.132x3+0.1x4+0.258x5+0.032x6+0.625x7+0.009x8-0.028x9+0.544x10
最后,利用各个公因子特征根的方差贡献率作为权重系数,得到因子分析的综合评价函数为:
综合得分F=F1* 78.364% +F2* 12.777%
四、回归分析
(一)模型摘要
表6 模型摘要
模型 | R | R方 | 调整后 R方 | 标准估算的错误 | 德宾-沃森 |
1 | .983a | .967 | .960 | 376.673 | .591 |
a. 预测变量:(常量), 国内生产总值(亿元) | |||||
b. 因变量:在售新房样本均价(元/平方米) | |||||
此处以在售新房样本均价为因变量,国内生产总值、居民消费水平、城镇人口数地产住宅投资、房地产开发企业土地成交价款、房地产开发投资额、居民销售价格指数、居民人均居住消费支出、房地产开发企业国内贷款、一年贷款利率作为自变量进行回归分析进行逐步加入回归分析。
回归分析得到国内生产总值作为自变量,在售新房样本均价为因变量的回归模型。其R方 =0.967,提示自变量可以解释96.7%的因变量(在售新房样本均价)变异,表示此回归分析有较好的拟合度。
(二)模型设计
表7 ANOVA
模型 | 平方和 | 自由度 | 均方 | F | 显著性 | |
1 | 回归 | 20785525.702 | 1 | 20785525.702 | 146.498 | .000b |
残差 | 709413.155 | 5 | 141882.631 | |||
总计 | 21494938.857 | 6 | ||||
a. 因变量:在售新房样本均价(元/平方米) | ||||||
b. 预测变量:(常量), 国内生产总值(亿元) | ||||||
如表7所示,结果显示,本研究回归模型具有统计学意义,F=146.498,P<0.001,提示因变量和自变量之间存在线性相关。系数见表8.
表8 回归系数
模型 | 未标准化系数 | 标准化系数 | t | 显著性 | ||
B | 标准错误 | Beta | ||||
1 | (常量) | 2580.793 | 822.589 | 3.137 | .026 | |
国内生产总值(亿元) | .013 | .001 | .983 | 12.104 | .000 | |
a. 因变量:在售新房样本均价(元/平方米) | ||||||
系数结果表显示,在回归方程中,国内生产总值的系数t=12.104, P=0.00<0.05 ,表示具有统计学意义。可以得到预测模型如下:
在售新房样本均价=2580.793 +0.013×国内生产总值
(三)模型检验
将收集到的数据代入到预测模型中,将得到的数据与真实值进行对比,并进行分析,见表9、图2。
表9 模型预测结果比较
年份 | 真实值 | 预测值 |
2010 | 9094 | 7938.3439 |
2011 | 9709 | 8924.0156 |
2012 | 9628 | 9582.3330 |
2013 | 10321 | 10289.3146 |
2014 | 10817 | 10947.1133 |
2015 | 10697 | 11535.9496 |
2016 | 12005 | 12283.9293 |
2017 | 13584 | 13397.2597 |
2018 | 14362 | 14531.4437 |
2019 | 14922 | 15462.0393 |
图2模型预测结果对比
验证结果分析,居民消费水平、城镇人口数地产住宅投资、房地产开发企业土地成交价款、房地产开发投资额、居民销售价格指数、居民人均居住消费支出、房地产开发企业国内贷款、一年贷款利率作为自变量引入模型时未出现统计学意义。其在售新房样本均价,主要受国内生产总值的影响。在售新房样本均价与国内生产总值产生挂钩关系,在关注在售新房样本均价,需持续关注国内生产总值。



